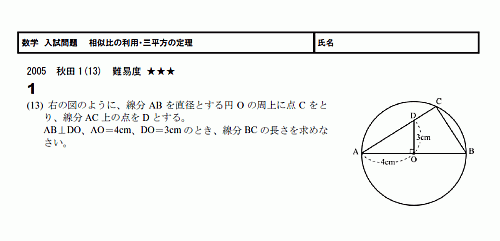
相似比の利用 三平方の定理 無料学習プリント教材
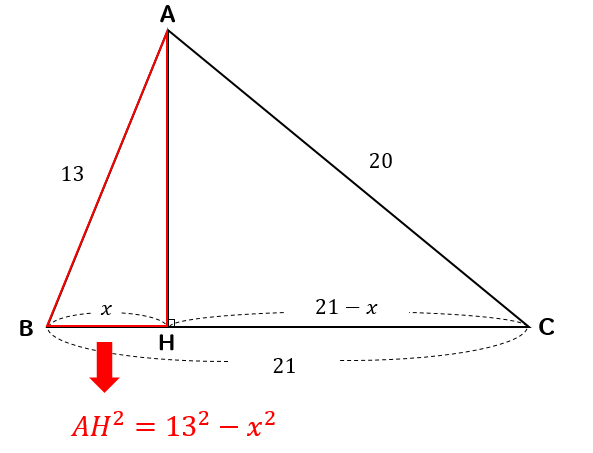
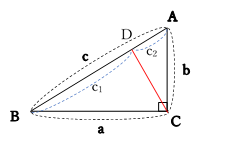
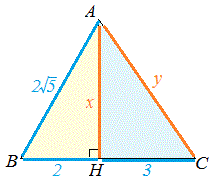
例3 右図で AC の長さは三平方の定理で求められるが, さらに相似図形の性質を使えば, ACBC=ABx になるので, x が求められる. (相似図形の性質をまだ習っていないときは こちらを先に 読む) 直角三角形 ABC に三平方の定理を適用すると 2152=AC2 AC2 三平方の定理を使って直角三角形の辺の長さを求める4つの問題 三平方の定理をつかった問題でよく出てくるのは、 直角三角形の辺の長さを求める問題。 今日はこの問題を4つのパターンに分けてみたぞ。 超基本タイプ 平方根の計算混じるタイプ 直角
三 平方 の 定理 応用
三 平方 の 定理 応用- このように、三平方の定理を使うためには 平方根(√)の扱いも大切になるので復習しておきましょう 。 2.三平方の定理の応用例 三平方の定理は数学における様々な場面で活躍します。意識していなくとも、数学をする上では必須の定理です。結晶構造の探究 ・・・・・・金児 正史 受験問題に盛り込まれた三平方の定理 ・・・・・・栗田 哲也 和算における三平方の定理 ・・・・・・小寺 裕 文献紹介・三平方の定理の一般化 ・・・・・・古藤 怜 二平方比の定理・三平方比の定理
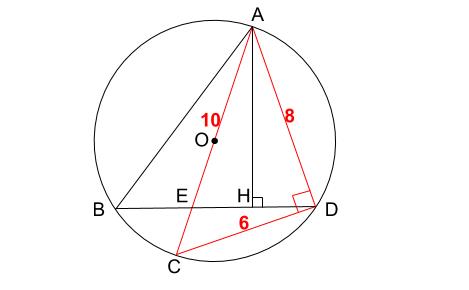
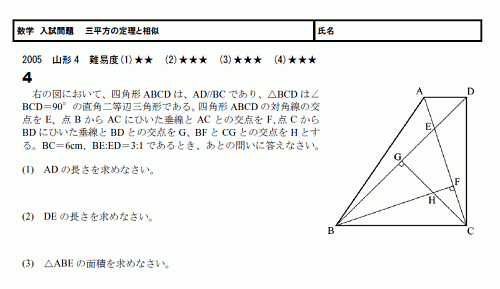
高校入試数学の難問 円 相似と三平方の定理の総合 中学数学の無料オンライン学習サイトchu Su
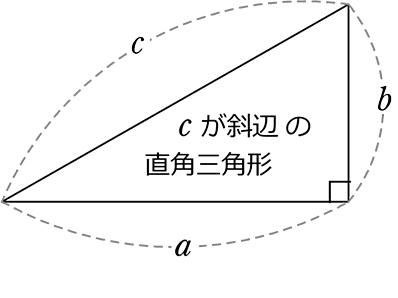
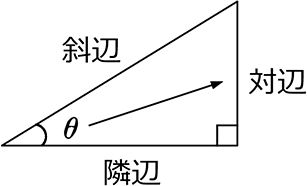
三平方の定理の証明 三平方の定理とは以下のように直角三角形ABCがあった時に、辺a(底辺)と辺b(高さ)の2つと辺c(斜辺)の関係性を以下のような等式で表した定理です。 公式:a²+b²=c² わかりやすく文章で表現しますと、 底辺の2乗と高さの2乗の 再び失礼致します. 今度はきちっと回答致します. 三平方の定理は,皆様のご回答の通り,幾何学的な問題に対して有効なものですが, #3さまのご回答にもありますように,電気回路を作るときにも用いられます. 電気回路に,抵抗・コンデンサ三平方の定理とは、古代ギリシアの数学者である「ピタゴラス」の名前を取って、「ピタゴラスの定理」と呼ぶこともある定理で、「直角三角形の3辺の長さの関係」表す定理です。 これですね。 2辺が直角 (すなわち90°)となるように接し、その2辺の端を
中村翔(逆転の数学) 「やり方を知り、練習する。 」 そうすれば、勉強は誰でもできるようになります。 机の勉強では、答えと解法が明確に決まっているからです。 「この授業動画を見たら、できるようになった! 」 皆さんに少しでもお役に立てる 三平方の定理とは 三平方の定理とは,直角三角形において各辺の関係は 斜辺 2 = 底辺 2 + 高さ 2 となる定理のことで、この定理のおかげで、 2辺の長さが分かればあと1辺の長さを求めることができる。AB=17cm, AC=10cm, BC=21cmの三角形 A B C 図は1辺4cmの正六角形である。 面積を求めよ。 図は一辺10cmの正八角形である。 面積を求めよ。 解説リクエスト 三平方の定理とは 三平方の定理 (基本問題1) 例題と練習 三平方の定理 (基本問題2) 例題と練習 三平方の
三 平方 の 定理 応用のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 | ||
 |  | |
 |  |  |
「三 平方 の 定理 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「三 平方 の 定理 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「三 平方 の 定理 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「三 平方 の 定理 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
「三 平方 の 定理 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
「三 平方 の 定理 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「三 平方 の 定理 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「三 平方 の 定理 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「三 平方 の 定理 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「三 平方 の 定理 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「三 平方 の 定理 応用」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |
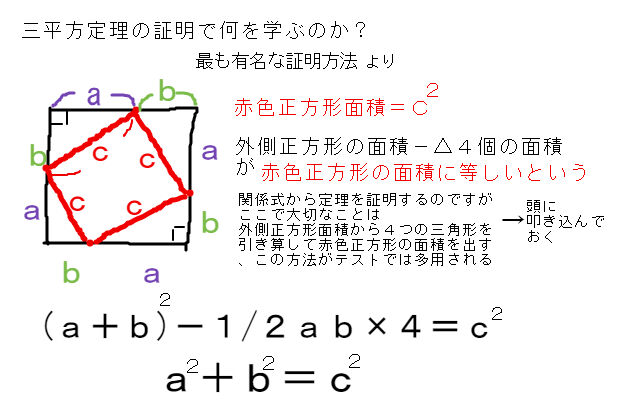
S,S,Sの関係は1 2 3 S+S=S1 2 3 三平方の定理 (ピタゴラスの定理) 直角三角形の直角をはさむ2辺の長さを , ,a b 斜辺の長さを とすると、次の関係が成り立つ。c a b c2+ =2 2 3つの2乗(平方)があるので、この名前がついている。 三平方の定理が成り立つことを証明するために、パズルを利用した面白い方法があります。 この方法であれば、数式を視覚的に理解でき、定理が成り立つ理由をよりイメージしやすくなります。 ここでは、パズルを使った証明の方法を紹介しましょう。 1





0 件のコメント:
コメントを投稿